QuantLib

New Semi-Analytic Heston Pricing Algorithms

hpcquantlibLeave a comment

The pricing engines for the Heston model in QuantLib have aged a bit. Meanwhile newer and better algorithms have been developed and discussed in the literature. For a comprehensive review please see [1][2]. Time to refurbish the existing engines.

The Heston model is defined by the following stochastic differential equation of the log spot

\begin{array}{rcl} d \ln S_t&=& \left(r_t - q_t - \frac{\nu_t}{2}\right)dt + \sqrt\nu_t dW^{S}_t \nonumber \\ d\nu_t&=& \kappa\left(\theta-\nu_t \right ) dt + \sigma\sqrt\nu_t dW^{\nu}_t \nonumber \\ \rho dt &=& dW^{S}_tdW^{\nu}_t \end{array}

The normalized characteristic function in the Gatheral formulation is given by

\phi_t(z) = \exp\left\{\frac{v_0}{\sigma^2}\frac{1-e^{-Dt}}{1-Ge^{-Dt}}\left(\kappa-i\rho\sigma z-D\right) + \frac{\kappa\theta}{\sigma^2}\left(\left(\kappa-i\rho\sigma z-D\right)t-2\ln\frac{1-Ge^{-Dt}}{1-G}\right) \right\}

\begin{array}{rcl} D&=&\sqrt{\left(\kappa - i\rho\sigma z\right)^2+\left(z^2+iz\right)\sigma^2} \nonumber \\ G&=&\displaystyle\frac{\kappa -i\rho\sigma z-D}{\kappa -i\rho\sigma z + D}\end{array}

Andersen and Piterbarg [3] introduced a Black-Scholes control variate to improve the numerical stability of Lewis’s formula (2001) for the price of a vanilla call option

\begin{array}{rcl} C(S_0, K, T)&=&BS\left(S_0, K, T, \sigma_{BS}\right) \nonumber \\ &+& \frac{\sqrt{Se^{(r-q)t}K}e^{-rt}}{\pi}\displaystyle\int\limits_{0}^{\infty}{\Re\left( \frac{\phi^{BS}_T\left(u-\frac{i}{2}\right) - \phi_T\left(u-\frac{i}{2}\right)}{u^2+\frac{1}{4}} e^{i u \left(\ln\frac{S}{K}+(r-q)T\right) } \right)  \mathrm{d}u}\end{array}

with the Black-Scholes price BS\left(S_0, K, T, \sigma_{BS}\right) of a vanilla call option with volatility \sigma_{BS} and the characteristic function

\phi^{BS}_T(z)=e^{-\frac{1}{2}\sigma_{BS}^2 T (z^2 + iz)}

Different proposals for the volatility of the vanilla option have been brought up in order to achieve an optimal control variate:

  • \sigma_{BS}^2 = \nu_0
  • \sigma_{BS}^2 = \frac{1}{\kappa t}\left(1-e^{-\kappa t}\right)\left(\nu_0-\theta\right) + \theta
  • \sigma_{BS}^2 = c_2 with c_2 the second cumulant of \ln \frac{F}{K} [1].

The diagram below shows the resulting integrand for the different control variate volatilities, the Heston model parameters

r=7.5\%, q=5\%, S_0=100, \nu_0=0.08, \rho=-80\%,\sigma=0.5, \kappa=4, \theta=0.05

and for a vanilla call option with strike K=200 and maturity t=2.0.

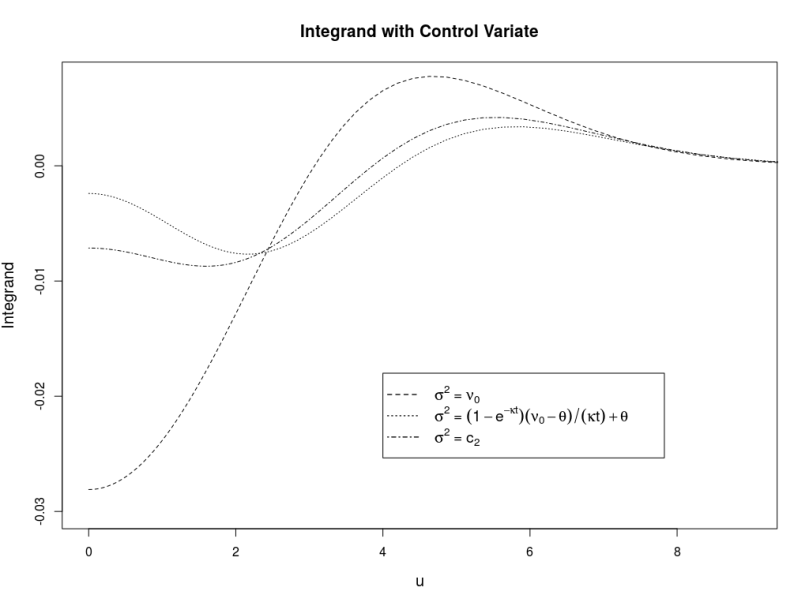
control_variate

The best choice depends on the Heston- and option parameters but it seems that

\sigma_{BS}^2 = \frac{1}{\kappa t}\left(1-e^{-\kappa t}\right)\left(\nu_0-\theta\right) + \theta

is a good option for a large variety of parameters. A direct comparison of the integrand with and without control variate shows how effective the control variate is.

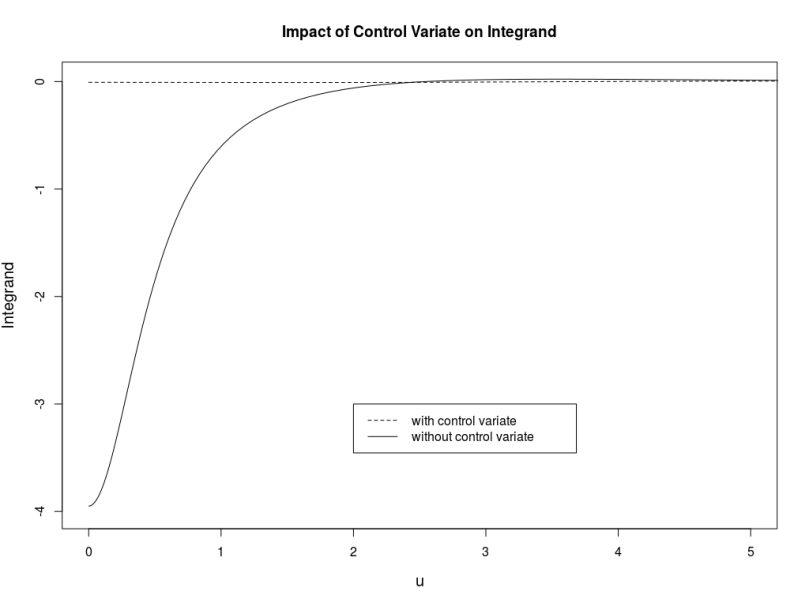
control_comparison

The central trick of Andersen-Piterbarg is now to truncate Lewis’s infinite integral at a finite u_{max} such that the remaining part is smaller than a given threshold based on the following inequation

\displaystyle\int_{u_{max}}^\infty \left\vert \frac{\phi_B(u-\frac{i}{2}) - \phi(u-\frac{i}{2})}{u^2+\frac{1}{4}} \right\vert du \le e^{-C_\infty u_{max}}\displaystyle\int_{u_{max}}^\infty \frac{1}{u^2} du

Please see the original paper or [2] for further details on how to get from here to an algorithm for u_{max}, especially for short dated options.

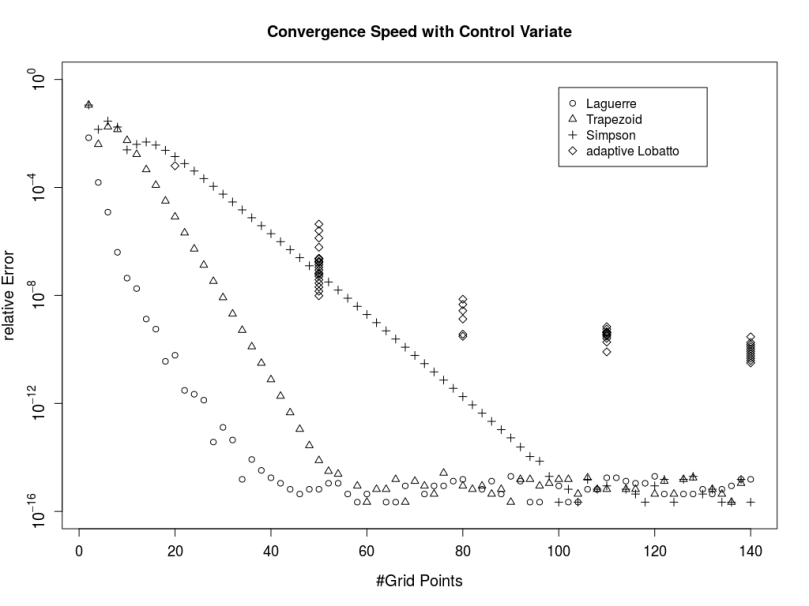
As Andersen and Piterbarg have pointed out, the simple trapezoidal rule works surprisingly well to carry out the resulting integral if a control variate is used. Alan Lewis’s test cases with high precision Heston reference prices should serve as a test bed here, in particular the call with strike 100. The Gauss-Laguerre method is very thankful for this particular test case but the point here is that the trapezoidal rule converges much faster than the higher order Simpson rule or the even more complex adaptive Gauss-Lobatto method.

convergence_speed

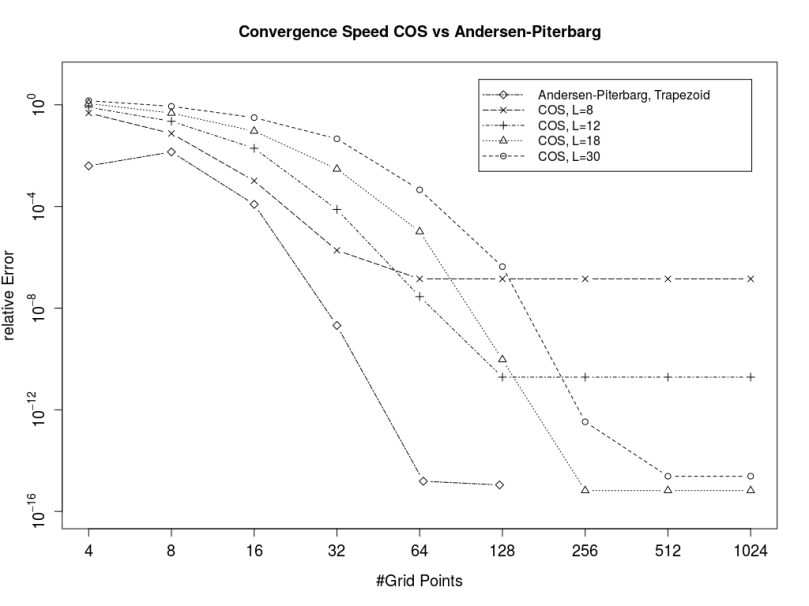
The diagram below compares the recently added COS engine with the Andersen-Piterbarg method using the trapezoid rule for this test-case. The Andersen-Piterbarg method is more accurate for a similar number of points.

convergence_comparison

The implementation is part of the pull request #251.

[1] M. Schmelzle, Option Pricing Formulae using Fourier Transform: Theory and Application.

[2] F. Le Floc’h, Fourier Integration and Stochastic Volatility Calibration.

[3] L. Andersen, and V. Piterbarg, 2010,  Interest Rate Modeling, Volume I: Foundations and Vanilla Models,  Atlantic Financial Press London.

Leave a comment